тема Непозиционные и позиционные системы счисления                https://ya.ru/video/preview/8629947983054744313 внимательно посмотреть видео

Прочтите, выпишите выделенное красным цветом.

Числа изображаются с помощью различных знаков – цифр. Определенный набор знаков составляют систему счисления.

Система счисления – совокупность приемов и правил записи чисел с помощью определенного набора символов.

На протяжении многовековой истории человечества существовало много различных систем счисления, некоторые дошли и до наших времен, а некоторые остались в истории и одна из них – единичная система счисления. Вспомните, как отвечает на вопрос о возрасте маленький ребенок?

Как вы учились считать в 1 классе? Так же, как и наши предки.

(на пальцах, с помощью счетных палочек)

На раскопках стоянок древних людей археологи находят изображения в виде засечек, черточек на твердых поверхностях: камне, глине, дереве – это так считали наши предки какие-то предметы, мешки, скот. Но записывать большие числа с помощью такой системы счисления неудобно, не так ли? И поэтому их начали группировать по 3, 5, 10 палочек. Так возникли более удобные системы счисления.

Из таких цифр строили свои числа древние египтяне. В такой записи чисел каждая цифра повторялась не более 9 раз, в противном случае эта запись заменялась одним вышестоящим числом.

У наших древних предков тоже была своя – древнерусская алфавитная система счисления. В качестве цифр наши предки использовали 27 букв кириллицы, только над ними для отличия ставили специальный знак – ТИТЛО.

А число 10000 обозначалось той же буквой, что и 1, только без титло, её обводили кружком и число называли “ТЬМОЙ”.

Самая большая из величин называлась “КОЛОДА” и она равнялась 10⁵⁰, считалось, что “БОЛЕЕ СЕГО НЕСТЬ ЧЕЛОВЕЧЕСКОМУ УМУ РАЗУМЕВАТИ”

Зависит ли от положения символа(цифры) в древнеегипетской, единичной, римской системах счисления ее значение?

нет

Действительно, все их можно объединить по одному признаку: позиция цифры в записи числа не влияет на её значение. Они получили название непозиционные системы счисления.

А как обстоит дело с арабскими цифрами, которые мы используем в жизни и на уроках математики?

(есть в учебниках, при подсчете, есть тема в 5-6 классах)

Вместе с непозиционными существуют и позиционные системы счисления. В них количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.

Примером позиционной системы счисления является вавилонская система счисления – шестидесятеричная. Кстати, мы с вами тоже ее используем. Вспомните, где?

(При измерении времени, углов.)

В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. Например, на Руси счет велся дюжинами. Английский фунт тоже равен 12 шиллингам. А где мы сегодня встречаемся с двенадцатеричной системой счисления? (предлагает сделать записи в тетрадь)

(Год – 12 месяцев, половина суток – 12 часов, сервизы и столовые приборы рассчитаны на 12 персон.)

Десятичная система счисления появилась в Индии в \/ в.н.э. и возникла она после появления цифры 0, которую придумали греческие астрономы для обозначения отсутствующей величины. Впоследствии с этой системой счисления познакомились арабы. Они по достоинству оценили её, начали использовать и в ХII веке завезли в Европу. И с этого времени человечество пользуется этой системой счисления. Цифры 10-ной СС называются арабскими, хотя начало они получили в Индии.

С появлением информатики, вычислительной техники нашла свое применение двоичная система счисления, корни которой уходят в древний Китай. Система гадания китайской Книги перемен при внимательном анализе обнаруживает в своей основе двоичную систему счисления и позиционный принцип записи чисел.

А почему её используют в информатике?

(Потому что компьютер – это электронное устройство. Это удобно отражать с помощью всего лишь двух цифр – 1 и 0).

В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.

Количество различных символов, используемых для изображения числа в позиционных системах счисления, называется основанием системы счисления. А множество всех символов, используемых для записи чисел в данной системе счисления – ее алфавитом.

Система счисления

Основание

Алфавит

Десятичная

10

0;1;2;3;4;5;6;7;8;9

Восьмеричная

8

0;1;2;3;4;5;6;7

Двоичная

2

0; 1

Шестнадцатеричная

16

0;1;2;3;4;5;6;7;8;9;A;B;C;D;E;F

Любое число можно представить в виде суммы произведений значащих цифр числа на степени основания СС. Такое представление называется развернутой формой записи числа.

155255₁₀ = 1 ·10⁵ + 5 ·10⁴ + 5 ·10³ + 2 ·10² + 5 ·10¹ + 5 ·10⁰

На этом принципе основан перевод чисел из любой СС в десятичную СС. Так, для перевода двоичного числа в десятичное нужно записать его в развернутой форме

111101₂ = 1 ·2⁵ + 1 ·2⁴ + 1 ·2³ + 1 ·2² + 0 ·2¹ + 1 ·2⁰ = 32 + 16 + 8 + 4 + 1 = 61₁₀

Перевод в десятичную СС

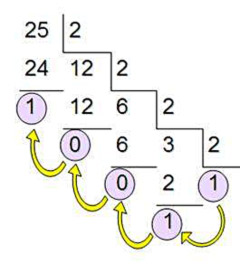Для обратного перевода десятичного числа в двоичное необходимо делить данное число на 2, фиксируя остатки. Деление продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Остатки записываются в обратном порядке

Пример: перевести число 25₁₀ из десятичной в двоичную:

25₁₀ = 11001₂

_{Домашнее задание:} § 1.1 с.6-15 прочесть, выписать понятия "позиционные" и "непозиционные" системы счисления